Classification using sequence, structure and dynamics distances

Release Notes

v2.4.1 series come with new and improved sequence, structure, and dynamics analysis features. See release notes for details.

How to Cite

Bakan A, Meireles LM, Bahar I ProDy: Protein Dynamics Inferred from Theory and Experiments
Bioinformatics 2011 27(11):1575-1577.

Bakan A, Dutta A, Mao W, Liu Y, Chennubhotla C, Lezon TR, Bahar I Evol and ProDy for Bridging Protein Sequence Evolution and Structural Dynamics
Bioinformatics 2014 30(18):2681-2683.

Zhang S, Krieger JM, Zhang Y, Kaya C, Kaynak B, Mikulska-Ruminska K, Doruker P, Li H, Bahar I ProDy 2.0: Increased scale and scope after 10 years of protein dynamics modelling with Python
Bioinformatics 2021 37(20):3657-3659.

Classification using sequence, structure and dynamics distances¶

We can compare the dynamics of individual proteins using the spectral overlap, also known as covariance overlap. The arccosine of this value provides a distance metric. Calculating this for all pairs in a mode ensemble gives us the spectral distance matrix, which can be used to calculate a dynamics-based “phylogenetic” tree. This can be compared against matrices and trees calculated using sequence and structure distances.

Again here are the imports if you need them.

In [1]: from prody import *

In [2]: from pylab import *

In [3]: ion()

Load PDBEnsemble and ModeEnsemble¶

We first load the PDBEnsemble:

In [4]: ens = loadEnsemble('LeuT.ens.npz')

Then we load the ModeEnsemble:

In [5]: gnms = loadModeEnsemble('LeuT.modeens.npz')

Spectral overlap and distance¶

We calculate a distance matrix based on spectral overlaps (calculated as their arccosines), calculate a tree from it and reorder the matrix using the tree as follows:

In [6]: sd_matrix = calcEnsembleSpectralOverlaps(gnms[:,:1], distance=True)

In [7]: labels = gnms.getLabels()

In [8]: so_tree = calcTree(names=labels,
   ...:                   distance_matrix=sd_matrix,
   ...:                   method='upgma')
   ...: 

In [9]: reordered_sd, new_sd_indices = reorderMatrix(names=labels,
   ...:                                              matrix=sd_matrix,
   ...:                                              tree=so_tree)
   ...: 

We can show the original and reordered spectral distance matrices and the tree as follows. showTree() has multiple format options. Here we show the output of using plt. This layout allows us to directly compare against the output from showMatrix() using the option origin=’upper’.

In [10]: showMatrix(sd_matrix, origin='upper');

In [11]: showTree(so_tree, format='plt');

In [12]: showMatrix(reordered_sd, origin='upper');

../../_images/ens_gnms_so_reordered_so_matrix.png

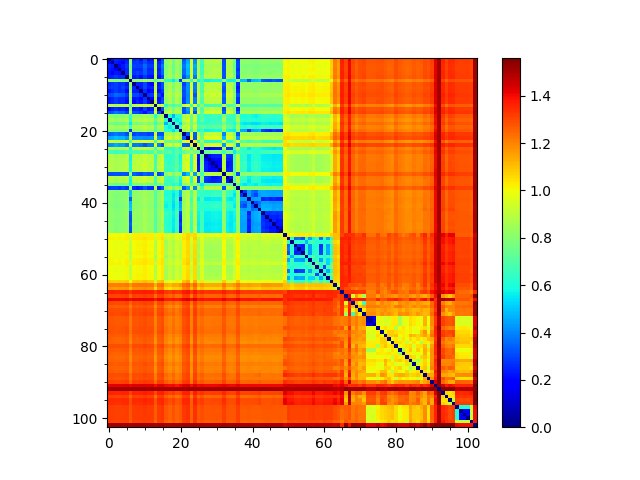
Sequence and structural distances¶

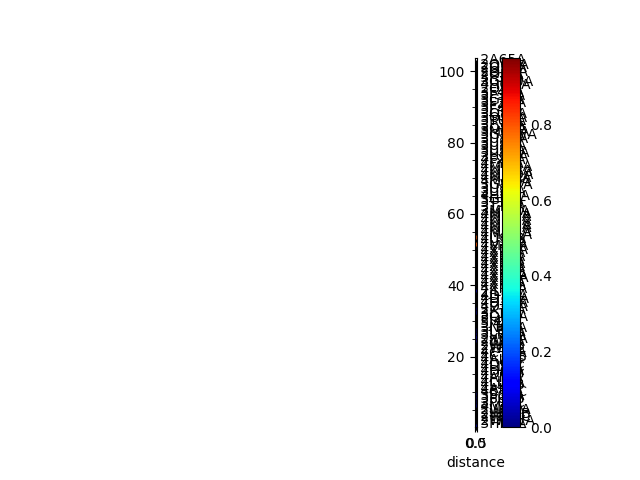
The sequence distance is given by the Hamming distance, which is calculated by subtracting the percentage identity (fraction) from 1, and the structural distance is the RMSD. We can also calculate and show the matrices and trees for these from the PDB ensemble.

In [13]: seqid_matrix = buildSeqidMatrix(ens.getMSA())

In [14]: seqd_matrix = 1. - seqid_matrix

In [15]: showMatrix(seqd_matrix, origin='upper');

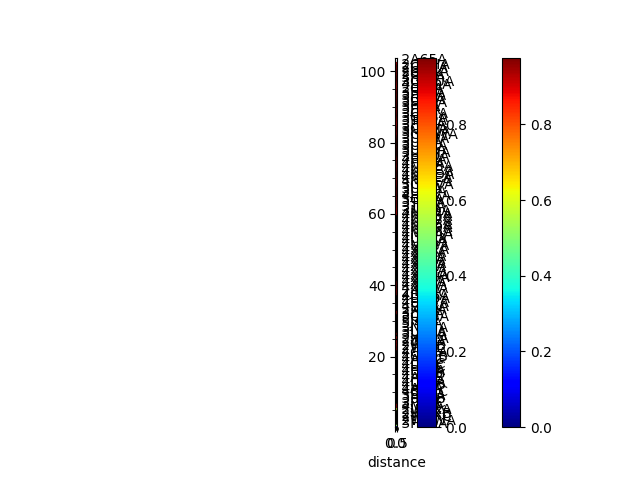
In [16]: seqd_tree = calcTree(names=labels,
   ....:                      distance_matrix=seqd_matrix,
   ....:                      method='upgma')
   ....: 

In [17]: showTree(seqd_tree, format='plt');

In [18]: reordered_seqd, indices = reorderMatrix(labels, seqd_matrix, seqd_tree)

In [19]: showMatrix(reordered_seqd, origin='upper');

../../_images/ens_gnms_seqd_reordered_seqd_matrix.png

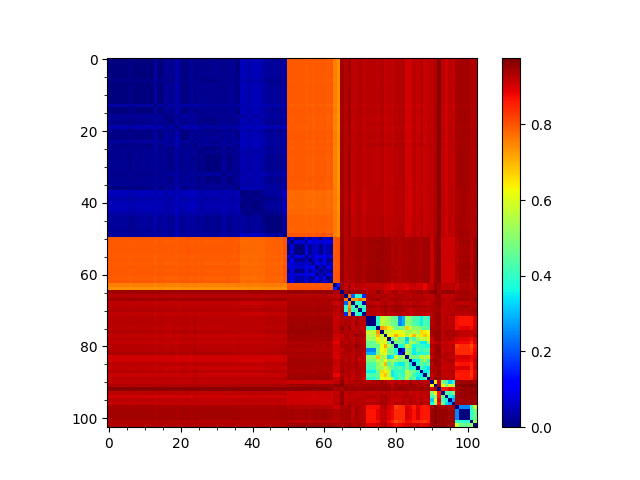
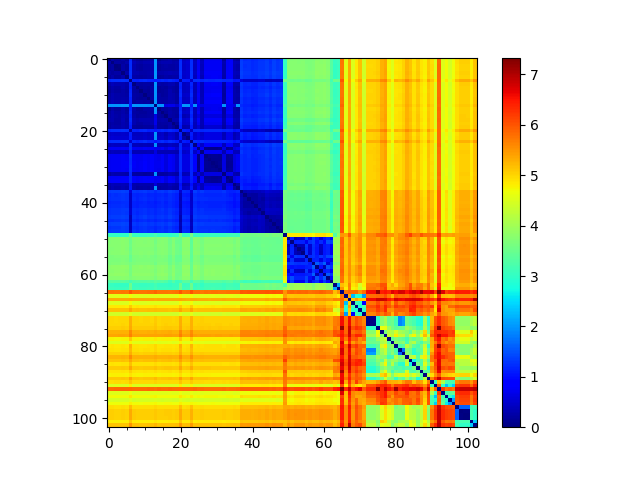
In [20]: rmsd_matrix = ens.getRMSDs(pairwise=True)

In [21]: showMatrix(rmsd_matrix, origin='upper');

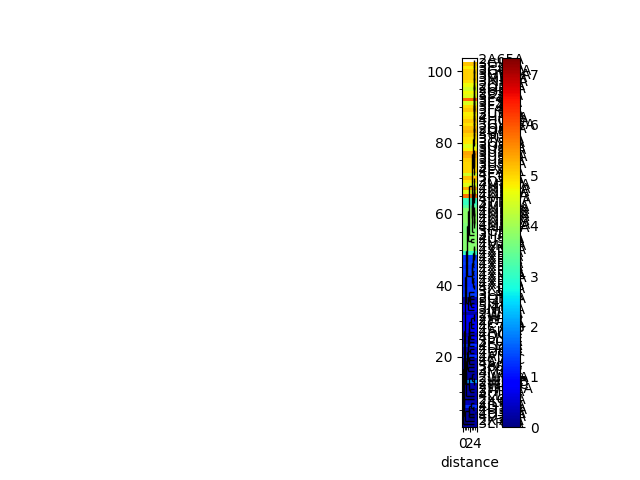
In [22]: rmsd_tree = calcTree(names=labels,
   ....:                      distance_matrix=rmsd_matrix,
   ....:                      method='upgma')
   ....: 

In [23]: showTree(rmsd_tree, format='plt');

In [24]: reordered_rmsd, indices = reorderMatrix(labels, rmsd_matrix, rmsd_tree)

In [25]: showMatrix(reordered_rmsd, origin='upper');

../../_images/ens_gnms_rmsd_reordered_rmsd_matrix.png

Comparing sequence, structural and dynamic classifications¶

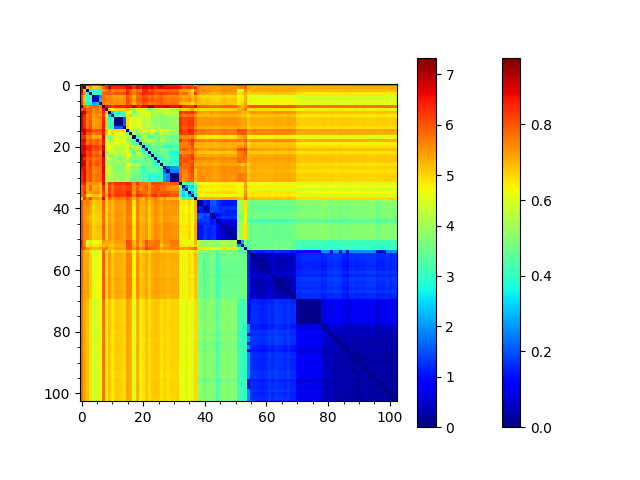
We can reorder the seqd and sod matrices by the RMSD tree too to compare them:

In [26]: reordered_seqd, indices = reorderMatrix(names=labels, matrix=seqd_matrix, tree=rmsd_tree)

In [27]: reordered_sd, indices = reorderMatrix(names=labels, matrix=sd_matrix, tree=rmsd_tree)

In [28]: showMatrix(reordered_seqd, origin='upper')
Out[28]: 
(<matplotlib.image.AxesImage at 0x7f4f1d7e1d50>,
 [],
 <matplotlib.colorbar.Colorbar at 0x7f4f1d779b10>)

In [29]: showMatrix(reordered_rmsd, origin='upper')
Out[29]: 
(<matplotlib.image.AxesImage at 0x7f4f1cb48690>,
 [],
 <matplotlib.colorbar.Colorbar at 0x7f4f1cb2fe50>)

In [30]: showMatrix(reordered_sd, origin='upper')
Out[30]: 
(<matplotlib.image.AxesImage at 0x7f4f1dae7bd0>,
 [],
 <matplotlib.colorbar.Colorbar at 0x7f4f1ca95410>)

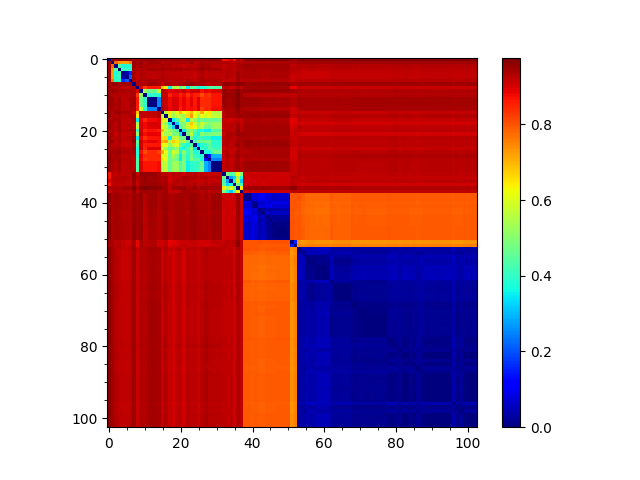
../../_images/ens_gnms_rmsd_reordered_seqd_matrix.png

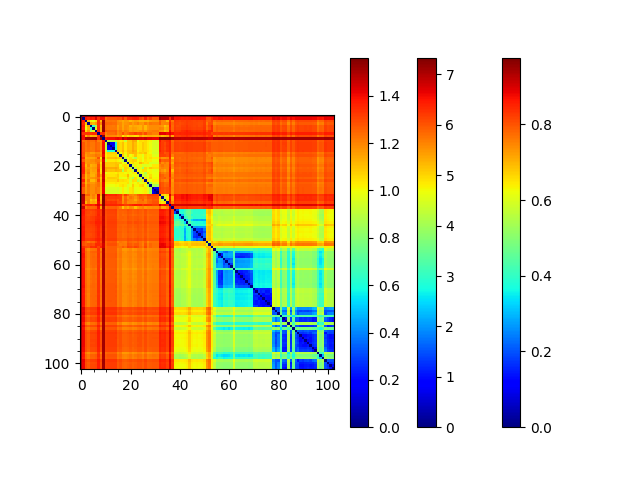
../../_images/ens_gnms_rmsd_reordered_sod_matrix.png

This analysis is quite sensitive to how many modes are used. As the number of modes approaches the full number, the dynamic distance order approaches the RMSD order. With smaller numbers, we see finer distinctions. This is particularly clear in the current case where we used just one mode.